Clustering

This blog is based on Jong-han Kim’s Linear Algebra

Clustering objective

$G_j \subset {1, \dots, N}$ is group $j$, for $j = 1, \dots, k$
$c_i$ is group that $x_i$ is in: $i \in G_{c_I}$
group representatives: $n$-vectors $z_1, \dots, z_k$
clustering objective is

\[J^{\text{clust}} = \frac{1}{N} \sum^N_{i=1}\lVert x_i - z_{c_i}\rVert^2\]

$J^{\text{clust}}$ small means good clustering
goal: choose clustering $c_i$ and representatives $z_j$ to minimize $J^{\text{clust}}$

Partitioning the vectors given the representatives

suppose representatives $z_1, \dots, z_k$ are given how do we assign the vectors to groups, i.e., choose $c_1, \dots, c_N$?

$c_i$ only appears in term $\lVert x_i - z_{c_i}\rVert^2 \ \text{in} \ J^{\text{clust}}$
to minimize over $c_i$, choose $c_i$ so $\lVert x_i - z_{c_i}\rVert^2 = \min_j{\lVert x_i - z_j\rVert^2}$

$k$-means algorithm

alternate between updating the partition, then the representatives
a famous algorithm called k-means
objective $J^{\text{clust}}$ decreases in each step

\[\begin{align*} &\text{given} \ x_1, \dots, x_N \in \mathbb{R}^n \ \text{and} \ z_1, \dots, z_k \in \mathbb{R}^n \\ &\text{repeat} \\ &\quad \text{Update partition: assign} i \ \text{to} \ G_j, j = \mathbf{argmin}_{j^\prime}\lVert x_i - z_j{^\prime}\rVert^2 \\ &\quad \text{Update centroids:} \ z_j = \frac{1}{\lvert G_j\rvert}\sum_{i \in G_j} x_i \\ &\text{until} \ z_1, \dots, z_k \text{stop changing} \end{align*}\]

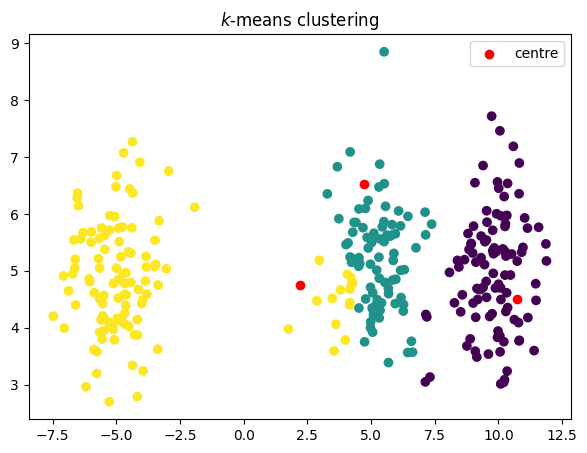
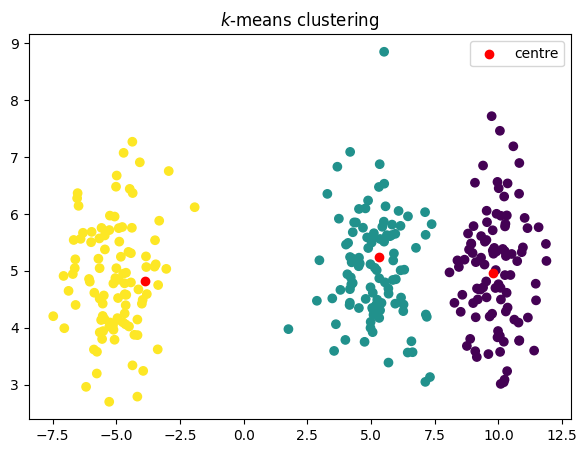
cluster1

코드

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(42)

data = np.concat([
  np.random.randn(100, 2) + (10, 5),
  np.random.randn(100, 2) + (5, 5),
  np.random.randn(100, 2) + (-5, 5)
])

init_centre = data[0:3]

print(init_centre)

def kmeans(k):
  for i in range(10):
    dist = np.sum(np.sqrt((data[:] - init_centre[:, np.newaxis])**2), axis=2)
    groups = np.argmin(dist, axis=0)

    print(groups)

    old_centroids = init_centre.copy()

    for i in range(k):
        if data[groups == i].shape[0] > 0:
            init_centre[i] = data[groups == i].mean(axis=0)

    if np.abs((init_centre - old_centroids).sum()) < 0.1:
      break

    plt.figure(figsize=(7, 5))
    plt.title("$k$-means clustering")
    plt.scatter(data[:, 0], data[:, 1], c=groups)
    plt.scatter(old_centroids[:, 0], old_centroids[:, 1], c="red", label="centre")
    plt.legend()
    plt.show()

kmeans(3)