Linear functions

This blog is based on Jong-han Kim’s Linear Algebra

Superposition and linear functions

$f: \mathbf{R}^n \rightarrow \mathbf{R}$
$f$ satisfies the superposition property if

\[f(\alpha x + \beta y) = \alpha f(x) + \beta f(y)\]
  • A function that satisfies superposition is called linear

linear verus affine

The inner product function

With $a$ an $n$-vector, the function

\[f(x) = a^Tx = a_1 x_1 + a_2 x_2 + \dots + a_n x_n\]

is the inner product function.

The inner product function is linear

\[\begin{align*} f(\alpha x + \beta y) &= a^T(\alpha x + \beta y) \\ &= a^T(\alpha x) + a^T(\beta y) \\ &= \alpha(a^T x) + \beta(a^T y) \\ &= \alpha f(x) + \beta f(y) \end{align*}\]

All linear functions are inner products

suppose $f: \mathbf{R}^n \rightarrow \mathbf{R}$ is linear
then it can be expressed as $f(x) = a^T x$ for some $a$
specifically: $a_i = f(e_i)$
follows from

\[\begin{align*} f(x) &= f(x_1e_1 + x_2e_2 + \dots + x_ne_n) \\ &= x_1f(e_1) + x_2f(e_2) + \dots + x_nf(e_n) \end{align*}\]

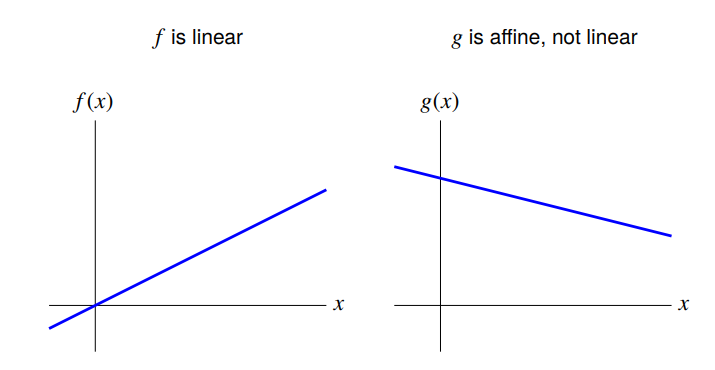
Affine functions

A function that is linear plus a constant is called affine.
General form is $f(x) = a^T x + b$, with $a$ an $n$-vector and $b$ a scalar
a function $f: \mathbf{R}^n \rightarrow \mathbf{R}$ is affine if and only if

\[f(\alpha x + \beta y) = \alpha f(x) + \beta f(y)\]

holds for all $\alpha, \beta$ with $\alpha + \beta = 1$, and all $n$-vectors $x, y$

First-order Taylor approximation

suppose $f: \mathbf{R}^n \rightarrow \mathbf{R}$
first-order Taylor approximation of $f$, near point $z$:

\[\hat{f}(x) = f(z) + \frac{\partial f}{\partial x_1}(z)(x_1 - z_1) + \dots + \frac{\partial f}{\partial x_n}(z)(x_n - z_n)\]

$\hat{f}(x)$ is very close to $f(x)$ when $x_i$ are all near $z_i$
$\hat{f}$ is an affine function of $x$ can write using inner product as

\[\hat{f}(x) = f(z) + \nabla f(z)^T(x - z)\]

where $n$-vector $\nabla f(z)$ is the gradient of $f$ at $z$,

\[\nabla f(z) = \left( \frac{\partial f}{\partial x_1}(z), \dots, \frac{\partial f}{\partial x_n}(z) \right)\]

Regression Model

regression model is (the affine function of $x$)

\[\hat{y} = x^T\beta + \nu\]
  • $x$ is a feature vector; its elements $x_i$ are called regressors
  • $n$-vector $\beta$ is the weight vector
  • scalar $\nu$ is the offset
  • scalar $\hat{y}$ is the prediction