Line, Line segment, Ray

직선(line), 선분(line segment), 반직선(ray)를 살펴보자.

Line은 두 점을 지나면서 양쪽 방향으로 무한히 커지는 선이다.
반면, line segment는 두 점 사이에서만 정의되는 선이다.
ray는 한 점에서 시작해서 다른 점을 지나면서 무한히 커지는 선을 말한다.

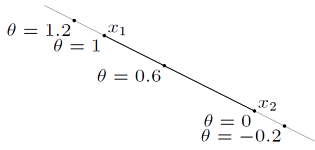
Line

두 점 $x_1$ 과 $x_2$ 을 지나는 Line은 다음과 같이 정의된다.

\(y = \theta x_1 + (1 - \theta) x_2 \quad \text{with} \quad \theta \in \mathbb{R}\) 여기서 $\theta$ 는 임의의 실수이며
$\theta$ 가 $0$ 이면 $y$ 는 $x_2$ 가 되고,
$\theta$ 가 $1$ 이면 $y$ 는 $x_1$ 이 된다. $\theta$ 가 $0$ 보다 작거나 $1$ 보다 크면 $x2$ 에서 $x_1$ 범위를 벗어난다.

Line segment

Line 식에서 $\theta$ 의 범위를 $0$ 에서 $1$ 로 제한하면 line segment이다.
따라서 line segment는 Line 식에 $0 \leq \theta \leq 1$ 조건 추가해 정의할 수 있다.

위 식을 변형하면 다음과 같이 표현 가능하다.

Ray

Ray는 한 점에서 시작해 다른 점을 지나면서 무한히 커지는 직선이다.
점 $x_2$ 에서 출발해서 $(x_1 - x_2)$ 벡터 방향으로 $\theta$ 배로 무한히 진행한다.

이 식을 정리하면 다음과 같다.