Convex set

Convex set은 오목하게 들어간 부분이나 내부에 구멍이 없는 집합을 의미한다. 따라서 어떤 집합이 convex set이라 말할 수 있으려면 집합에 속한 임의의 두 점으로 선분(line segment)을 만들어서 그 선분이 집합에 포함되는지를 보면 된다.

Convex set

집합 $C \subseteq \mathbb{R}^n$ 에 속한 두 점 $x_1, x_2 \in C$ 을 연결한 line segment가 $C$ 에 포함되면 이 집합을 convex set이라고 한다.

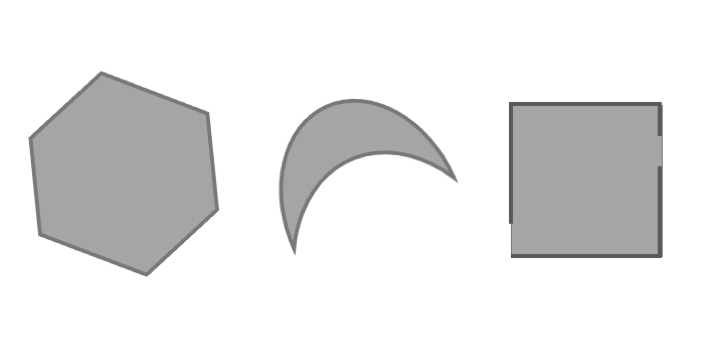
위 그림에는 convex set을 설명하는 예들이 있다. 왼쪽의 육각형은 convex이지만 가운데에 있는 콩팥 모양은 내부에 두 점을 이었을 때 선분이 외부로 나가기 때문에 convex가 아니다. 오른쪽 네모의 경우 경계의 일부가 open된 상태라서 경계에서 선분을 만들면 set의 범위를 벗어나므로 convex가 아니다.

Convex combination

점들을 linear combination할 때 계수가 양수이고 계수의 합을 1로 제한하면 이를 convex combination이라고 한다.

이제 convex set의 정의를 convex combination 개념을 이용해서 일반화해 볼 수 있다. 즉, 어떤 집합 $C$ 에 속하는 임의의 여러 점들의 convex combination이 집합 $C$ 에 속하면 그 집합은 convex set이라고 말할 수 있다.

Convex hull

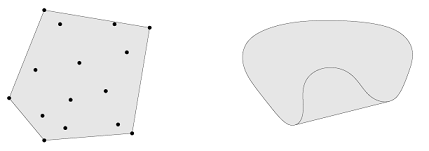
$C \subseteq \mathbb{R}^n$ 에 포함된 점들이 모든 convex combination들의 집합을 $C$ 의 convex hull이라고 하며 $\text{conv} \ C$ 로 표기한다. Convex hull $\text{conv}\ C$ 은 항상 convex이며, 집합 $C$ 를 포함하는 가장 작은 convex set이다.

\(\text{conv}\ C = \{\theta_1 x_1 + \dots + \theta_k x_k\ |\ x_i \in C, \theta_i \geq 0,\ i = 1, \dots, k,\ \theta_1 + \dots + \theta_k = 1\}\) 아래 그림은 15개의 점으로 이뤄진 집합과 콩팥 모양의 집합에 대한 convex hull이다.