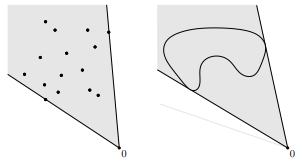
Cone
어떤 집합이 cone이라고 말할 수 있으려면 원점에서 집합에 속한 임의의 한 점을 지나는 반직선(ray)을 만들어서 그 반직선이 집합에 포함되는지를 보면 된다. (따라서 Cone은 반드지 원점을 포함해야 된다.) Cone은 경계를 가지므로 affine set이 될 수 없다.
참고: 01-02 Affine set
Cone
Cone은 반드시 원점을 포함해야 한다. 따라서 원점에서 시작해서 집합에 속한 점 $x \in C$ 을 지나는 ray를 만들었을 때 $\theta x \in C$ 가 되면 집합 $C$ 를 cone 또는 nonnegative homogenous라고 한다.
\[\theta x \in C\ \text{with}\ x \in C,\ \theta \geq 0\]Homogenous 뜻
여기서 homogenous는 크기(scale)만 바꿔도 성질이 변하지 않는다. 간단히 말해 배율만 바뀐다고 해석하면 된다.
- 수학에서 homogeneous
함수 $f(x)$ 가 homogeneous (of degree 1) 라는 말은
\(f(\lambda x) = \lambda f(x) \quad \forall\lambda\)
즉,
- 입력을 $\lambda$ 배 하면
- 출력도 $\lambda$ 배
- 집합에서 homogeneous 집합 $C$ 가 homogeneous 하다는 말은
\(x \in C \rightarrow \lambda x \in C\) 즉,
- 한 점이 들어 있으면
- 그 점의 스케일 버전도 계속 들어 있음
- Nonnegative homogeneous 여기서 nonnegative가 붙으면 이해하기 쉬워진다.
\(x \in C \rightarrow \theta x \in C \quad \forall\theta \geq 0\) 즉,
원점에서 한 방향으로만 스케일에 대해 닫혀 있다.
고 해석할 수 있다.
Convex Cone
집합 $C$ 가 cone이면서 동시에 convex이면 이를 convex cone이라고 한다.
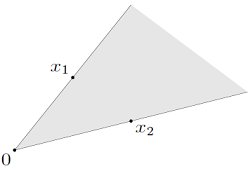
\(\theta_1 x_1 + \theta_2 x_2 \in C\ \text{with}\ x_1, x_2 \in C,\ \theta_1, \theta_2 \geq 0\) 다음 그림에서는 파이 모양의 convex cone을 보여주고 있다. 그림에서 $x_1$과 $x_2$는 경계에 속하는 점으로 $\theta_1$과 $\theta_2$가 모두 $0$이면 꼭지점이 되고, 둘 중 하나가 $0$이면 경계선이 되며, 둘 모두 $0$보다 크면 내부의 점이 된다.
Conic combination
여러 점들을 linear combination할 때 계수를 $0$이상으로 제한하게 되면 이를 conic combination 또는 nonnegative linear combination이라고 한다.
\(\text{A point of the form}\quad \theta_1 x_1 + \theta_2 x_2 + \dots + \theta_k x_k\ \text{with}\ \theta_i \geq 0,\ i = 1, \dots, k\) 이제 cone 정의를 conic combination 개념을 이용해서 일반화해 볼 수 있다. 즉, 어떤 집합 $C$에 속하는 임의의 여러 점들을 conic combination했을 때, 그 결과가 다시 집합 $C$에 속하면 그 집합은 conic set이라고 말할 수 있다.
Conic hull
$C \subseteq \mathbb{R}^n$ 에 포함된 점들의 모든 conic combination들의 집합을 $C$ 의 conic hull이라고 한다. Conic hull은 항상 집합 $C$ 를 포함하는 가장 작은 convex cone이다.